
Ils sont les milliards mais ils sont peu nombreux. Dans l'imensité des entiers, ils sont moins de 3%. Ils sont étudiés depuis des siècles par les mathématiciens les plus célèbres mais aucun d'eux n'a trouvé une méthode pour les calculer et les identifier de manière fiable et rapide.
Les plus grands nombres premiers connus dépassent des centaines de millers de chiffres pour ma part, je ne m'intéresse à des nombres premiers un peu particuliers. Les nombres premiers qui sont des palindrommes comme 101000011111110000101 ou 155555555555555555551. Et également des nombres premiers cycliques tels que 23456789123456789123. Mais pourquoi ? parcequ'ils sont faciles à retenir.
Mon nombre premier préféré est le 2. Il n'y pas plus puissant que ce nombre. A lui tout seul, il réduit à néant l'espoir de 50% des nombres d'entrer dans le club très fermé des nombres premiers. De plus, il a le mérite d'être le premier ce que beaucoup aimeraient bien être, moi y compris. Certains diront qu'il n'est que le deuxième, après le un. Je ne vais pas me lancer dans une démonstration mathématique par l'absurde qui n'a rien à faire dans mes pages Web mais je ne pense pas qu'il faille le considérer comme un nombre premier. La définition dit "un nombre est premier s'il n'est divisible que par 1 et lui-même". L'application de la définition pour "1" donne "1 est premier car il n'est divisible que par 1 et 1". Le "que par 1 et 1" ne sonne pas bien à mes oreilles logiques. Car si 1 et 1 ne sont pas distincts et ne font qu'un, "1" n'est pas premier car il n'y a pas deux diviseurs. Et, si "1 et 1" font 2 (encore lui !) je me demande le résultat pourrait avoir l'addition de "1" et de l'autre "1". Je me range donc dans la catégorie de ceux qui pensent que le chiffre 1 n'est pas premier. Pour donner un peu d'eau à leur moulin je rajouterai que si "1" était réellement un nombre premier la décomposition d'un nombre en facteurs premiers comporterait toujours le 1^0. Chose que je n'est jamais vu faire.... les choses sont-elles claires ?
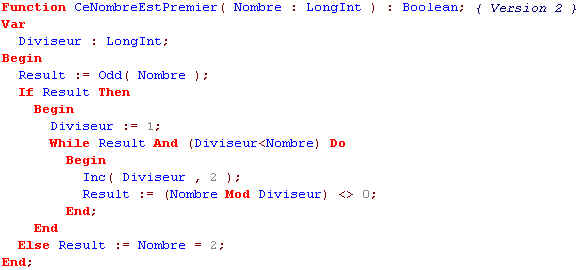
La méthode la plus simple pour tester la primalité d'un nombre est de le diviser par tous les nombres qui lui sont inférieurs et de regarder si le reste est nul ou pas. Le problème de cette méthode est qu'elle est lente puisque pour tester un nombre n il faut faire n-2 divisions.



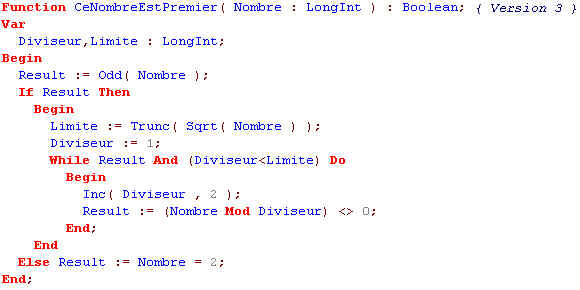
Ce qui fait Sqrt(n)/2 calculs; c'est cette dernière amélioration qui fait que cet algorithme est, malgré sa simplicité, efficace pour les petits nombres du type LongInt du pascal.
| Nombre n a tester | Nombre de divisions Algo1 | Nombre de divisions algo 2 | Nombre de divisions algo 3 | |
| Tableau | 100 | 98 | 50 | 5 |
| 1000 | 998 | 500 | 16 | |
| comparatif | 10000 | 9998 | 5000 | 50 |
| 100000 | 99998 | 50000 | 158 | |
| de la vitesse | 1000000 | 999998 | 500000 | 500 |
| 10000000 | 9999998 | 5000000 | 1581 | |
| des 3 algo. | 100000000 | 99999998 | 50000000 | 5000 |
| 1000000000 | 999999998 | 500000000 | 15811 |
2- Les problêmes...
J'était arrivé à ce stade lors de l'achat de mon premier PC. Celui-ci, équipé d'un disque dur et d'un Basic compilé m'a permis de calculer plus vite mais comme les nombres premiers s'accumulaient plus vite et la place nécessaire pour les stocker aussi. Il y a en effet plus 5 750 000 nombres premiers parmis les 100 premiers Millions entiers naturels, à raison de 4 octets par nombre premier je voyait bien que mon beau disque dur de 20Mo serait bien vite saturé. Il fallait trouver une solution pour réduire la taille de stockage. J'ai pensé dans un premier temps à la solution qui consiste à ne stocker que les différences entre les nombres premiers ce qui aurait eu l'effet de diviser la taille de stockage par 4. Cette taille pouvait même être divisée par 8 en divisant la différence par 2. Mais, en extrapolant, ma nouvelle limite se situait aux alentours des 800 Millions et non pas 2 Milliards, le but que je m'étais fixé. Cette solution était en plus très lente lors de la relecture des nombre et impliquait de lire les nombres de manière chronologique et de partir toujours du premier. Ne trouvant pas de solution et voyant bien que je demandais trop à mon premier PC le projet est tombé aux oubliettes.
3- L'idée de base...
C'est dans une bibliothèque qu'une idée a germée dans mon esprit aride. Pourquoi ne pas stocker les nombres de manière binaire ? 0=le nombre est premier, 1 il ne l'est pas. La suite 2,3,5,7,11,13,17,19,23,29,31 pouvait être codée en 10010101 11010111 01011101 11110101 ou 95 D7 5D F5 soit un stockage de 12 nombres sur 4 octets. Bien sûr, pour des nombres plus grands, les 4 octets ne stockeraient pas autant de nombres. Avec cette méthode, 500000 nombres étaient réprésentés par 62500 octets ce qui n'était pas suffisant car par rapport à ma première méthode je perdais de la place dès les premiers millons. C'est à ce moment que j'ai commencé à beaucoup aimer le "2" car si je ne tenais pas compte de tout les nombres pairs ce n'était plus 500000 nombres mais 1 Million de nombres qui étaient représentés dans 62500 octets.
Cette idée, le nouveau PC acheté en peu avant, le nouveau Turbo Pascal et pkzip allaient relancer, ce que ma famille appelle mon obsession. Un petit calcul rapide 2Millards / 1Million = 2000, 2000 * 62500 = 125Millions d'octets pour un disque de 240Mo c'était jouable...Le portage des applications écrites en Turbo Basic en Pascal n'a pas posé de problème particulier mais, un fois les 2 Milliards atteints et écrits sur moins de 75Mo grâce à pkzip et ceci en quelques semaines de calcul. Jai épprouvé des nouvelles frustrations. Et, encore lui, elles étaient "2". La première était la lenteur de calcul et la seconde la limite des 2147483647 (2^31-1) du longInt.
4- De la suite dans les idées de base...
Pour résoudre la première, je n'avait pas trente six solutions, il fallait trouver un nouvel algorithme. Il fallait soit diminuer le nombre de calculs soit faire des calculs plus simples. Des recherches dans les livres de la bibliothèque locale m'ont permis de trouver le plus vieil algorithme connu : "le crible d'érastotène". Cet algo, adapté à mes tableaux binaires, est simple car il ne comporte quasiment que des additions qui sont moins gourmandes en temps CPU que les divisions extrèment nombreuses dans non premier algorithme.
le principe du criblage adapté à mes besoins sans l'optimisation du "2":
On écrit des nombres dans un tableau linéaire :
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
On prend tous les nombres premiers inférieurs à la racine carrée du plus grand soit, dans notre exemple 11 ce qui donne 2,3,5,7,11
On prend le premier nombre : le "2" et on calcul son premier multiple dans l'intervalle 100..130 soit 100 et on coche la case et les multiples suivants jusqu'à ce que le multiple sorte de l'intervalle. ce qui donne :
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
On prend le premier nombre : le "3" et on calcul son premier multiple dans l'intervalle 100..130 soit 102 et on coche la case et les multiples suivants :
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
Au final le tableau devient :
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
Pour calculer le premier impact, il faut une division. Et pour les impacts suivant sont obtenus par une addition. En plus, on ne teste que les nombres premiers inférieurs à la racine carrée du max et non pas tous les nombres impairs qui sont au moins dix fois plus nombreux.
Au final, la vitesse de cet algorithme est environ 20 fois plus rapide que le premier et quelques heures suffirent à tester les 2 premiers milliards. Il doit cependant être initialiser par la connaissance des premiers nombres premiers et, c'est la seule chose à laquelle me sert désormais le premier de mes algorithmes recherche de nombres premiers.
5- Plus de limites.
Pour passer le cap du LongInt, à l'époque de Delphi 2 et 3 sur le tout nouveau PC Bi-Pentium, je n'ai pas eu d'autre solution que de réaliser mes propres bibliothèques et mes propres objets. L'ohjet remplaçant du LongInt que j'ai appelé le THugeInt devait pouvoir réaliser les quatres opérations arithmétiques de base et posséder une fonction modulo et une fonction racine carré. L'option choisie a été de stocker le nombre par paquets de quatre chiffres dans un tableau de LongInt. Le choix du longInt pour ne stocker que 4 digits peut sembler bizarre mais pour les calculs intermédiaires lors des multiplications il évite les Range Check Error.
Bien sûr il a fallu des fonctions booléennes Pair/impair, Nul/non nul, égal/différent, Supérieur/inférieur et des méthodes de remise à zero, de division et de multiplication par dix et de copie pour que THugeInt soit un objet utilisable. La méthode la plus difficile à mettre au point fut la fonction racine carrée car il a fallu, tout d'abord, réfléchir. La racine carrée d'un nombre entier n n'exite par forcément dans le nomde des entiers, il fallait la majorer d'un pour des raisons de sureté. Son résultat était donc compris entre "2" (encore et toujours lui) et n-1.
La dichotomie m'a semblée être une solution rapide comme dans bien des cas. Mais pour un nombre comme un millard il fallait déjà trentes itérations pour aboutir au résultat. Cette perpective laissait présager un nombre de calculs assez astronomiques pour des nombres de 20 ou 30 chiffres. Pour palier à la lenteur de l'algo, il fallait optimiser son initialisation. La racine carrée d'un nombre A de n chiffres comporte approximativement n/2 chiffres. Pour être plus strict si n est pair la racine carrée comporte n/2 chiffres et dans le cas contraire elle comporte (n+1)/2 chiffres. En prenant le min et le max des nombres comportants n/2 ou (n+1)/2 chiffres comme initialisation de l'algo ce dernier devient plus rapide. Je suis sûr qu'il existe une méthode plus rapide mais je ne l'ai pas encore trouvée.
Le THugeInt développé et testé, il a fallu développer l'objet Crible servant à gérer le stockage de l'intervalle de un million de nombres, a passer en revue multiples des nombres pour effacer leurs multiples et à sauvegarder le résultat dans un fichier. Ce fichier sera d'ailleurs comprimé lors de la sortie de delphi 3 grâce à l'unité ZLib qui remplaça avantageusement les appels à pkzip/unzip en version share...
5- De nouveaux problêmes.
L'étape suivante, consistait en la réalisation du programe calculant les cribles contenant les nombres premiers et d'un programme de consultation. Le premier programme, déstiné à tourner en permanence ne devait sutout pas rallentir la machine et l'apprentissage des Threads c'est avéré être plutôt plaisant. Aujourd'hui j'ai réussi, le tout en moins de 3Go à stocker tous les nombres premiers inférieurs à 100 Milliards et, faute de place, j'ai dù stopper les recherches.... Mais les nombres calculés peuvent servir à tester des nombres de plus de 20 chiffres en quelques milliards de calculs par la méthode des divisions et avec baeucoup de patience. Malgré les améliorations par rapport à mon premier algorithme, l'algorithme est lent mais pas dans le même référentiel...
6- Conclusion.
Les diverses étapes décrites ont occupé mon esprit des heures et des heures pendant des années (plus de 15 !). Je crois que j'ai réalisé mon rêve d'enfant car pour stocker et calculer de nouveaux nombres premiers je ne suis plus limité que par l'espace disque de mon micro que mon porte monnaie et ma raison (qui a tort) m'interdissent de changer. La vitesse de l'algo de criblage est très stable par rapport au rang du million testé. Le BI pentium m'a également permis de réaliser un programme en "réseau" permettant d'accroître encore la vitesse des tests des grands nombres.
7- Le futur ?
Il m'arrive encore trop souvent de tester un nombre pendant des jours pour m'appercevoir qu'il n'est pas premier. Je suis donc en train de développer le test de Fermat qui, malgré le fait qu'il ne soit pas toujours juste, devrait me permettre de résoudre cette grande frustration. J'explore aussi d'autres tests, beaucoup plus rapides car plus mathématiques et moins systématiques. Les recherches ne sont plus réalisées dans les bibliothèques mais dans les pages WEB avec toujours la même difficulté qui consiste à la recherche de l'information... J'aimerait aussi installer mes programmes sur un réseau de plusieurs centaines de postes juste pour occuper leurs petits processeurs qui ne font rien 95% de leur temps...